Table of contents
No headings in the article.
🎯What is RSA encryption?
👉RSA (Rivest-Shamir-Adleman) is an algorithm used for secure data transmission. It is an asymmetric encryption that is widely used for secure data transmission.
👉In RSA, each person has a pair of keys: a public key and a private key.
👉The public key can be shared with anyone, while the private key must be kept secret.
👉When a message is sent using RSA, the sender encrypts the message using the recipient's public key.
👉The recipient then decrypts the message using their private key.
👉This ensures that only the intended recipient can read the message, as only they have the private key needed to decrypt it.
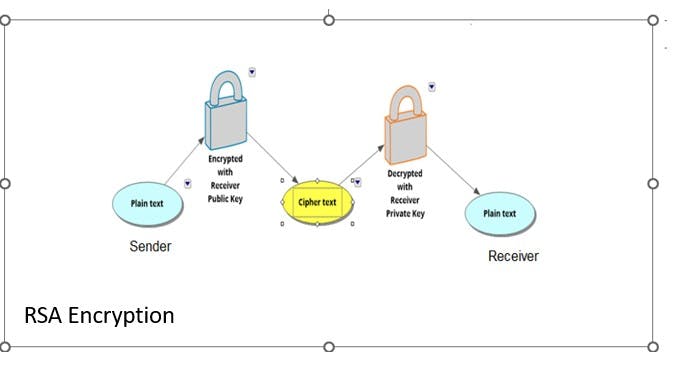
📌A simple demonstration of how the RSA algorithm works
🌲Suppose Swetha wants to send a secure message to Vijay.
🌲Vijay generates a pair of keys using the RSA algorithm and sends his public key to Swetha.
🌲Swetha uses Vijay's public key to encrypt her message and sends the encrypted message (ciphertext) to Vijay.
🌲Vijay then uses his private key to decrypt the ciphertext and read the original message (plaintext).
📌Key generation:
🌲Vijay selects two prime numbers, p, and q, and calculates n = p *q and in this example, p = 5 and q = 11, so n = 5 *11 = 55.
🌲Vijay calculates a value called the totient, denoted as φ(n), which is the number of positive integers less than n that are relatively prime to n. In this case, φ(55) = (p - 1) (q - 1) = 4 *10 = 40.
🌲The factors of 40 are 2*2*2*5.
🌲Vijay selects a public key, e, that is relatively prime to φ(n) and none of the factors of 2 and 5. In this example, let's say e =7.
🌲Vijay calculates his private key, d, such that e d ≡ 1 (mod φ(n)) or we can derive d= (1+ x φ(n))/e while x can be 0,1,2, 3, etc.
After some calculations using Excel, d is calculated as d = (1+4*40)/7 = 23.
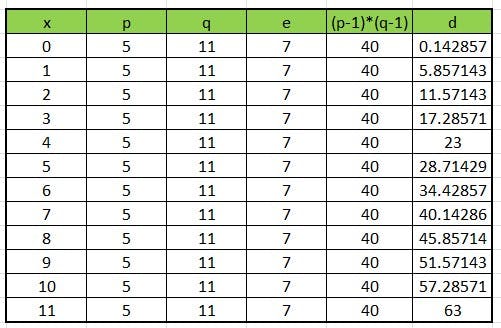
🌲We now have n=55, e=7, d=23
🌲Vijay's public key is the pair (e, n), and his private key is the pair (d, n). Vijay sends his public key to Swetha.
📌Encryption:
🌲Swetha wants to send the message "HELLO" to Vijay.
🌲She converts the message using a predetermined scheme (e.g., A=1, B=2, till Z=26.).
🌲Swetha calculates the ciphertext, c, using the formula c ≡ m^e (mod n), where m is the plain text.
🌲In this case, c is calculated as c = 8^7 (mod 55) 5^7 (mod 55) 12^7 (mod 55) 12^7 (mod 55) 15^7 (mod 55).
🌲c= 2 25 23 23 5. Swetha sends the ciphertext to Vijay.
📌Decryption:
🌲Vijay receives Swetha's ciphertext, 2 25 23 23 5.
🌲Vijay calculates the plaintext, m, using the formula m = c^d (mod n).
🌲In this case, m = 2^23 (mod 55) 25^23 (mod 55)23^23 (mod 55)23^23 (mod 55)5^23 (mod 55) = 8 5 12 12 15.
🌲Vijay converts the number back to the message "HELLO" using the predetermined scheme.
👉The link for the calculation is a calculator.
🎯Below are the screenshots of the Python code used to create the RSA public, private, encryption, and decryption algorithms.
👉Please refer to the link to generate RSA keys using python RSA Keygen
🎯The Public and Private key Generation

🎯Encryption Algorithm

🎯Decryption Algorithm

🌲Strengths
👉When compared to symmetric encryption, there is no need to exchange the keys ahead of time.
👉"Non-repudiation" is achieved because data cannot be changed during communication.
👉It's a one-way function, so knowing one prime key won't get you the other primes.
🌲Weakness
👉The difficulty of generating keys.
👉The RSA algorithm is relatively slow when compared to symmetric algorithms.
Community and Social Footprints:

